1. The area of a rectangle with sides x and 3x, is how many times greater than the area of a right angled isosceles triangle with side x?
2. If $81 is to be divided among n people, where n > 1, so that each gets $x, where x is a whole number > 1, how many different values could there be for n?
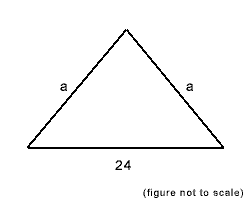
3. If the area of the triangle shown above is 108 square centimeters, what is its perimeter in centimeters?
4. A charity organisation sells greetings cards in packs costing $10 or $2.50 each. A total of 75 packs were sold at a fair for a total of $375. How many of the $2.50 packs were sold?
5. The length of a rectangle is 2/7 of the perimeter. What is the value of the diagonal of the rectangle if the perimeter is 14 units?
6. A = {A, B, C, D, E, F, G}
B = {0, 1, 2}
C = {1, 2, 3, 4, 5, 6, 7, 8, 9}
The filing system in an office requires each file to have an alphanumeric code name of the form abc. A, B and C are the sets from which a,b, and c must be chosen. How many possible code names are there?
7. A measuring cylinder is filled one third full with ethanol. A mixture of ethanol, water and propanol is used to fill the measuring flask to capacity. What fraction of the final mixture is ethanol?
8. The equation y = 6 is graphed on the same coordinate axes as the circle with center (4,4) and radius 3.
One of the points of intersection of the line and the circle has x-coordinate 1.76. What is the x coordinate of the other point of intersection?
9. If a and b are positive integers, and (ab3/2)2 = 108, what is the value of ab?
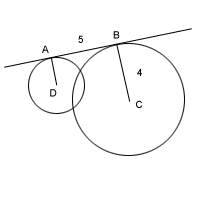
10. The line through AB is tangent to two circles with centers D and C and whose areas are in the ratio 4: 1
If AB = 5 and BC =4, what is the length of line segment DC (not shown)? Grid your answer correct to three significant figures.












