一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设全集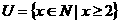 ,集合
,集合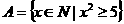 ,则
,则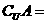 ( )
( )
A. 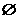 B.
B. 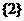 C.
C. 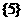 D.
D. 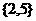
【答案】B
【解析】
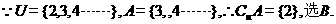
(2)已知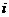 是虚数单位,
是虚数单位,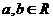 ,则“
,则“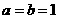 ”是“
”是“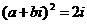 ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】

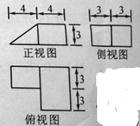
(3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是
A. 90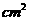 B. 129
B. 129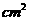 C. 132
C. 132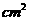 D. 138
D. 138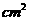
【答案】D
【解析】

4.为了得到函数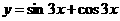 的图像,可以将函数
的图像,可以将函数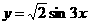 的图像( )
的图像( )
A.向右平移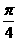 个单位 B.向左平移
个单位 B.向左平移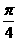 个单位
个单位
C.向右平移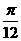 个单位 D.向左平移
个单位 D.向左平移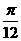 个单位
个单位
【答案】C
【解析】
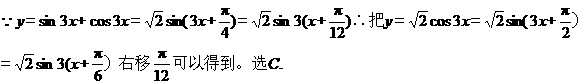
5.在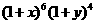 的展开式中,记
的展开式中,记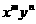 项的系数为
项的系数为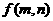 ,则
,则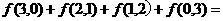 ( )
( )
A.45 B.60 C.120 D. 210
【答案】C
【解析】
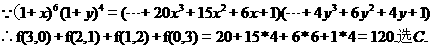
6.已知函数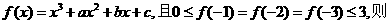 ( )
( )
A.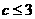 B.
B.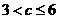 C.
C.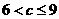 D.
D. 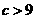
【答案】C
【解析】
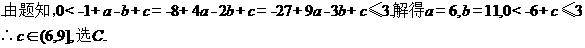
7.在同意直角坐标系中,函数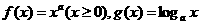 的图像可能是( )
的图像可能是( )
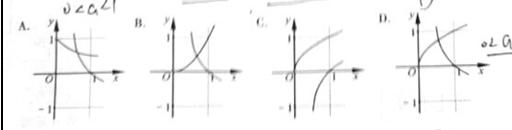
【答案】D
【解析】

8.记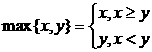 ,
,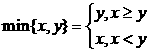 ,设
,设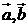 为平面向量,则( )
为平面向量,则( )
A.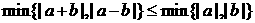
B.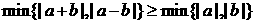
C.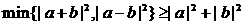
D.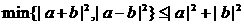
【答案】D
【解析】

9.已知甲盒中仅有1个球且为红球,乙盒中有 个红球和
个红球和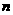 个篮球
个篮球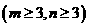 ,从乙盒中随机抽取
,从乙盒中随机抽取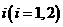 个球放入甲盒中.
个球放入甲盒中.
(a)放入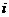 个球后,甲盒中含有红球的个数记为
个球后,甲盒中含有红球的个数记为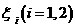 ;
;
(b)放入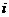 个球后,从甲盒中取1个球是红球的概率记为
个球后,从甲盒中取1个球是红球的概率记为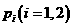 .
.
则
A.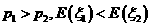 B.
B.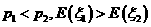
C.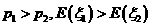 D.
D.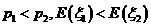
【答案】A
【解析】

10.设函数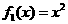 ,
,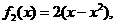
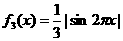 ,
,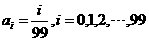 ,记
,记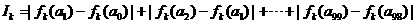 ,
,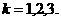 则
则
A.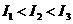 B.
B. 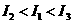 C.
C. 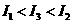 D.
D. 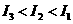
【答案】 B
【解析】

二、填空题:本大题共7小题,每小题4分,共28分.
11.若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是________.
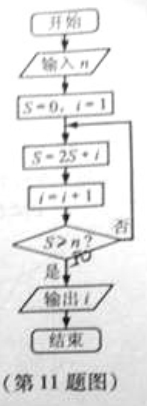
【答案】 6
【解析】

12.随机变量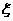 的取值为0,1,2,若
的取值为0,1,2,若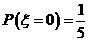 ,
,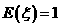 ,则
,则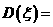 ________.
________.
【答案】 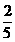
【解析】
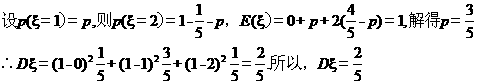
13.当实数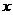 ,
,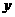 满足
满足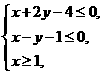 时,
时,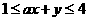 恒成立,则实数
恒成立,则实数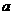 的取值范围是________.
的取值范围是________.
【答案】 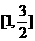
【解析】

14.在8张奖券中有一、二、三等奖各1张,其余5张无奖.将这8张奖券分配给4个人,每人2张,不同的获奖情况有_____种(用数字作答).
【答案】 60
【解析】
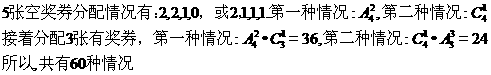
15.设函数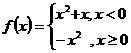 若
若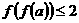 ,则实数
,则实数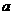 的取值范围是______
的取值范围是______
【答案】 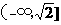
【解析】

16.设直线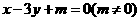 与双曲线
与双曲线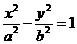 (
(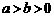 )两条渐近线分别交于点
)两条渐近线分别交于点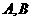 ,若点
,若点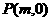 满足
满足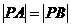 ,则该双曲线的离心率是__________
,则该双曲线的离心率是__________
【答案】 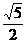
【解析】

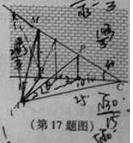
17、如图,某人在垂直于水平地面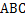 的墙面前的点
的墙面前的点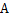 处进行射击训练.已知点
处进行射击训练.已知点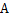 到墙面的距离为
到墙面的距离为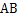 ,某目标点
,某目标点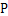 沿墙面的射击线
沿墙面的射击线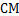 移动,此人为了准确瞄准目标点
移动,此人为了准确瞄准目标点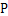 ,需计算由点
,需计算由点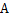 观察点
观察点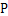 的仰角
的仰角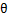 的大小.若
的大小.若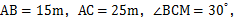 则
则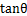 的最大值
的最大值
【答案】 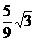
【解析】

三.解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)在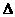 ABC中,内角A,B,C所对的边分别为a,b,c,已知
ABC中,内角A,B,C所对的边分别为a,b,c,已知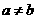 ,
,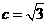 ,
,
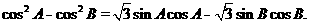
(I) 求角C的大小;
(II) 若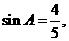 求
求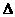 ABC的面积。
ABC的面积。
【答案】
(1) 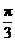 (2)
(2) 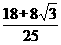
【解析】
(1)
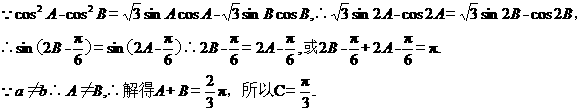
(2)
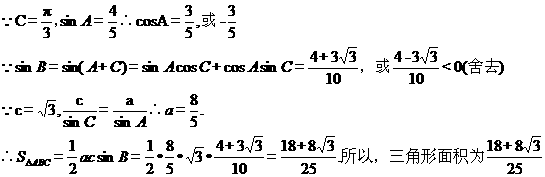
19(本题满分14分)
已知数列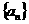 和
和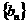 满足
满足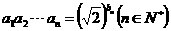 .若
.若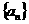 为等比数列,且
为等比数列,且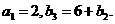
(1)求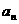 与
与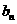 ;
;
(2)设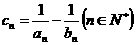 。记数列
。记数列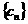 的前
的前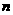 项和为
项和为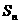 .
.
(i)求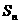 ;
;
(ii)求正整数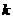 ,使得对任意
,使得对任意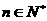 ,均有
,均有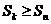 .
.
【答案】
(1) 省略 (2) 4
【解析】
(1)
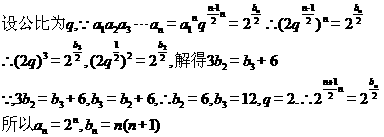
(2)

20. (本题满分15分)如图,在四棱锥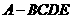 中,平面
中,平面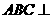 平面
平面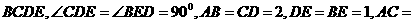
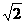 .
.
(1)证明: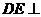 平面
平面 ;
;
(2)求二面角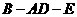 的大小
的大小
【答案】
[ Ⅰ ] 省略 [ Ⅱ ] 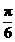
【解析】
[ Ⅰ ]

[ Ⅱ ]

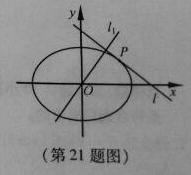
21(本题满分15分)
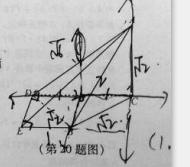
如图,设椭圆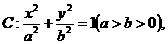 动直线
动直线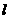 与椭圆
与椭圆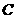 只有一个公共点
只有一个公共点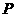 ,且点
,且点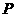 在第一象限.
在第一象限.
(1)已知直线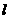 的斜率为
的斜率为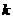 ,用
,用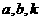 表示点
表示点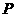 的坐标;
的坐标;
(2)若过原点 的直线
的直线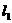 与
与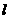 垂直,证明:点
垂直,证明:点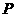 到直线
到直线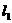 的距离的最大值为
的距离的最大值为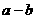 .
.
【答案】
[ Ⅰ ] 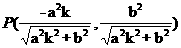 [ Ⅱ ] 省略
[ Ⅱ ] 省略
【解析】
[ Ⅰ ]

[ Ⅱ ]

22.(本题满分14分)已知函数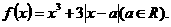
(1)若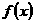 在
在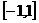 上的最大值和最小值分别记为
上的最大值和最小值分别记为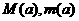 ,求
,求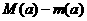 ;
;
设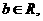 若
若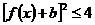 对
对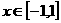 恒成立,求
恒成立,求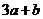 的取值范围.
的取值范围.
【答案】 [ Ⅰ ]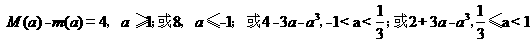
[ Ⅱ ] [-2, 0]
【解析】
[ Ⅰ ]
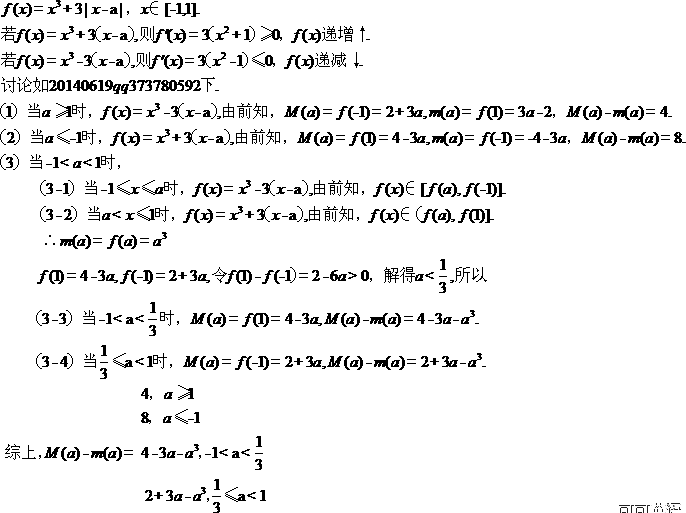
[ Ⅱ ]













