第 卷(选择题 共50分)
卷(选择题 共50分)
一. 选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. [2014·安徽卷] 设i是虚数单位,复数i3+=( )
A.-i B.i C.-1 D.1
1.D [解析] i3+=-i+=1.
2. [2014·安徽卷] 命题“∀x∈R,|x|+x2≥0”的否定是( )
A.∀x∈R,|x|+x2<0
B.∀x∈R,|x|+x2≤0
C.∃x0∈R,|x0|+x<0
D.∃x0∈R,|x0|+x≥0
2.C [解析] 易知该命题的否定为“∃x0∈R,|x0|+x<0”.
3. [2014·安徽卷] 抛物线y=x2的准线方程是( )
A.y=-1 B.y=-2
C.x=-1 D.x=-2
3.A [解析] 因为抛物线y=x2的标准方程为x2=4y,所以其准线方程为y=-1.
4. [2014·安徽卷] 如图11所示,程序框图(算法流程图)的输出结果是( )
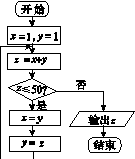
图11
A.34 B.55 C.78 D.89
4.B [解析] 由程序框图可知,列出每次循环过后变量的取值情况如下:
第一次循环,x=1,y=1,z=2;
第二次循环,x=1,y=2,z=3;
第三次循环,x=2,y=3,z=5;
第四次循环,x=3,y=5,z=8;
第五次循环,x=5,y=8,z=13;
第六次循环,x=8,y=13,z=21;
第七次循环,x=13,y=21,z=34;
第八次循环,x=21,y=34,z=55,不满足条件,跳出循环.
5. [2014·安徽卷] 设a=log37,b=21.1,c=0.83.1,则( )
A.b<a<c B.c<a<b
C.c<b<a D.a<c<b
5.B [解析] 因为2>a=log37>1,b=21.1>2,c=0.83.1<1,所以c<a<b.
6. [2014·安徽卷] 过点P(-,-1)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是( )
A. B.
C. D.
6.D [解析] 易知直线l的斜率存在,所以可设l:y+1=k(x+),即kx-y+k-1=0.因为直线l圆x2+y2=1有公共点,所以圆心(0,0)到直线l的距离≤1,即k2-k≤0,解得0≤k≤,故直线l的倾斜角的取值范围是.
7. [2014·安徽卷] 若将函数f(x)=sin 2x+cos 2x的图像向右平移φ个单位,所得图像关于y轴对称,则φ的最小正值是( )
A. B.
C. D.
7.C [解析] 方法一:将f(x)=sin的图像向右平移φ个单位,得到y=sin的图像,由所得图像关于y轴对称,可知sin=±1,即sin=±1,故2φ-=kπ+,k∈Z,即φ=+,k∈Z,又φ>0,所以φmin=.
8. [2014·安徽卷] 一个多面体的三视图如图12所示,则该多面体的体积是( )
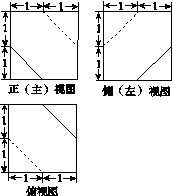
图12
A. B. C.6 D.7
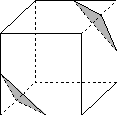
8.A [解析] 如图所示,由三视图可知该几何体是棱长为2的正方体截去两个小三棱锥后余下的部分,其体积V=8-2×××1×1×1=.
9. [2014·安徽卷] 若函数f(x)=|x+1|+|2x+a|的最小值为3,则实数a的值为( )
A.5或8 B.-1或5
C.-1或-4 D.-4或8
9.D [解析] 当a≥2时,
f(x)=
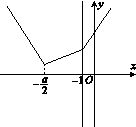
由图可知,当x=-时,fmin(x)=f=-1=3,可得a=8.
当a<2时,f(x)
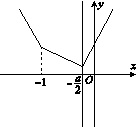
由图可知,当x=-时,fmin(x)=f=+1=3,可得a=-4.综上可知,a的值为-4或8.
10. [2014·安徽卷] 设a,b为非零向量,|b|=2|a|,两组向量x1,x2,x3,x4和y1,y2,y3,y4均由2个a和2个b排列而成,若x1·y1+x2·y2+x3·y3+x4·y4所有可能取值中的最小值为4|a|2,则a与b的夹角为( )
A. B. C. D.0
10.B [解析] 令S=x1·y1+x2·y2+x3·y3+x4·y4,则可能的取值有3种情况:S1=2+2,S2=++2a·b,S3=4a·b.又因为|b|=2|a|.所以S1-S3=2a2+2b2-4a·b=2>0,S1-S2=a2+b2-2a·b=(a-b)2>0,S2-S3=(a-b)2>0,所以S3<S2<S1,故Smin=S3=4a·b.设a,b的夹角为θ,则Smin=4a·b=8|a|2cos θ=4|a|2,所以cos θ=.又θ∈[0,π],所以θ=.
11. [2014·安徽卷] +log3+log3=________.
11. [解析] 原式= +log3==.
12. [2014·安徽卷] 如图13,在等腰直角三角形ABC中,斜边BC=2,过点A作BC的垂线,垂足为A1;过点A1作AC的垂线,垂足为A2;过点A2作A1C的垂线,垂足为A3;….依此类推,设BA=a1,AA1=a2,A1A2=a3,…,A5A6=a7,则a7=________.
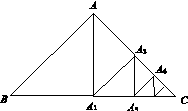
图13
12. [解析] 在等腰直角三角形ABC中,斜边BC=2 ,所以AB=AC=a1=2,由题易知A1A2=a3=AB=1,…,A6A7=a7=·AB=2×=.
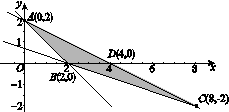
13. [2014·安徽卷] 不等式组表示的平面区域的面积为________.
13.4 [解析] 不等式组所表示的平面区域如图中阴影部分所示,S△ABD=S△ABD+S△BCD=×2×(2+2)=4.
14. [2014·安徽卷] 若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=则f+f=______.
14. [解析] 由题易知f+f=f+f=-f-f=-+sin=.
15. [2014·安徽卷] 若直线l与曲线C满足下列两个条件:
(i)直线l在点P(x0,y0)处与曲线C相切;(ii)曲线C在点P附近位于直线l的两侧.则称直线l在点P处“切过”曲线C.
下列命题正确的是________(写出所有正确命题的编号).
①直线l:y=0在点P(0,0)处“切过”曲线C:y=x3;
②直线l:x=-1在点P(-1,0)处“切过”曲线C:y=(x+1)2;
③直线l:y=x在点P(0,0)处“切过”曲线C:y=sin x;
④直线l:y=x在点P(0,0)处“切过”曲线C:y=tan x;
⑤直线l:y=x-1在点P(1,0)处“切过”曲线C:y=ln x.
15.①③④ [解析] 对于①,因为y′=3x2,y′x=0=0,所以l:y=0是曲线C:y=x3在点P(0,0)处的切线,画图可知曲线C在点P附近位于直线l的两侧,①正确;
对于②,因为y′=2(x+1),y′x=-1=0,所以l:x=-1不是曲线C:y=(x+1)2在点P(-1,0)处的切线,②错误;
对于③,y′=cos x,y′x=0=1,所以曲线C在点P(0,0)处的切线为l:y=x,画图可知曲线C在点P附近位于直线l的两侧,③正确;
对于④,y′=,y′x=0=1,所以曲线C在点P(0,0)处的切线为l:y=x,画图可知曲线C在点P附近位于直线l的两侧,④正确;
对于⑤,y′=,y′x=1=1,所以曲线C在点P(1,0)处切线为l:y=x-1,又由h(x)=x-1-ln x(x>0)可得h′(x)=1-=,所以hmin(x)=h(1)=0,故x-1≥ln x,所以曲线C在点P附近位于直线l的下侧,⑤错误.
16. [2014·安徽卷] 设△ABC的内角A,B,C所对边的长分别是a,b,c,且b=3,c=1,△ABC的面积为.求cos A与a的值.
16.解: 由三角形面积公式,得
×3×1·sin A=,故sin A=.
因为sin2A+cos2A=1,
所以cos A=±=±=±.
①当cos A=时,由余弦定理得a2=b2+c2-2bccos A=32+12-2×1×3×=8,
所以a=2 .
②当cos A=-时,由余弦定理得a2=b2+c2-2bccos A=32+12-2×1×3×=12,所以a=2 .
17. [2014·安徽卷] 某高校共有学生15 000人,其中男生10 500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图14所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估计该校学生每周平均体育运动时间超过4小时的概率.
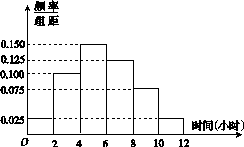
图14
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2=
17.解: (1)300×=90,所以应收集90位女生的样本数据.
(2)由频率分布直方图得每周平均体育运动超过4小时的频率为1-2×(0.100+0.025)=0.75,所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.
(3)由(2)知,300位学生中有300×0.75=225(位)的每周平均体育运动时间超过4小时,75人的每周平均体育运动时间不超过4小时.又因为样本数据中有210份是关于男生的,90份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 45 | 30 | 75 |
每周平均体育运动时间超过4小时 | 165 | 60 | 225 |
总计 | 210 | 90 | 300 |
结合列联表可算得K2==≈4.762>3.841.
所以有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
18. [2014·安徽卷] 数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N*.
(1)证明:数列是等差数列;
(2)设bn=3n·,求数列{bn}的前n项和Sn.
18.解: (1)证明:由已知可得=+1,即-=1,所以是以=1为首项,1为公差的等差数列.
(2)由(1)得=1+(n-1)·1=n,所以an=n2,
从而可得bn=n·3n.
Sn=1×31+2×32+…+(n-1)×3n-1+n×3n,①
3Sn=1×32+2×33+…+(n-1)3n+n×3n+1.②
①-②得-2Sn=31+32+…+3n-n·3n+1=-n·3n+1=,
所以Sn=.
19. [2014·安徽卷] 如图15所示,四棱锥P ABCD的底面是边长为8的正方形,四条侧棱长均为2.点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
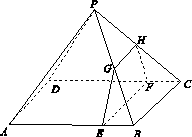
图15
(1)证明:GH∥EF;
(2)若EB=2,求四边形GEFH的面积.
19.解: (1)证明:因为BC∥平面GEFH,BC⊂平面PBC,且平面PBC∩平面GEFH=GH,所以GH∥BC.
同理可证EF∥BC,因此GH∥EF.
(2)连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
因为PA=PC,O是AC的中点,所以PO⊥AC,同理可得PO⊥BD.又BD∩AC=O,且AC,BD都在平面ABCD内,所以PO⊥平面ABCD.
又因为平面GEFH⊥平面ABCD,
且PO⊄平面GEFH,所以PO∥平面GEFH.
因为平面PBD∩平面GEFH=GK,
所以PO∥GK,所以GK⊥平面ABCD.
又EF⊂平面ABCD,所以GK⊥EF,
所以GK是梯形GEFH的高.
由AB=8,EB=2得EB∶AB=KB∶DB=1∶4,
从而KB=DB=OB,即K是OB的中点.
再由PO∥GK得GK=PO,
所以G是PB的中点,且GH=BC=4.
由已知可得OB=4,PO===6,
所以GK=3,故四边形GEFH的面积S=·GK=×3=18.
20. [2014·安徽卷] 设函数f(x)=1+(1+a)x-x2-x3,其中a>0.
(1)讨论f(x)在其定义域上的单调性;
(2)当x∈[0,1]时,求f(x)取得最大值和最小值时的x的值.
20.解: (1)f(x)的定义域为(-∞,+∞),
f′(x)=1+a-2x-3x2.
令f′(x)=0,得x1=,
x2=,且x1<x2,
所以f′(x)=-3(x-x1)(x-x2).
当x<x1或x>x2时,f′(x)<0;
当x1<x<x2时,f′(x)>0.
故f(x)在和 内单调递减,
在内单调递增.
(2)因为a>0,所以x1<0,x2>0,
①当a≥4时,x2≥1,由(1)知,f(x)在[0,1]上单调递增,所以f(x)在x=0和x=1处分别取得最小值和最大值.
②当0<a<4时,x2<1,由(1)知,f(x)在[0,x2]上单调递增,在[x2,1]上单调递减,
因此f(x)在x=x2=处取得最大值.又f(0)=1,f(1)=a,
所以当0<a<1时,f(x)在x=1处取得最小值;
当a=1时,f(x)在x=0和x=1处同时取得最小值;
当1<a<4时,f(x)在x=0处取得最小值.
21. [2014·安徽卷] 设F1,F2分别是椭圆E:+=1(a>b>0)的左、右焦点,过点F1的直线交椭圆E于A,B两点,|AF1|=3|F1B|.
(1)若|AB|=4,△ABF2的周长为16,求|AF2|;
(2)若cos∠AF2B=,求椭圆E的离心率.
21.解:(1)由|AF1|=3|F1B|,|AB|=4,得|AF1|=3,|F1B|=1.
因为△ABF2的周长为16,所以由椭圆定义可得4a=16,所以|AF1|+|AF2|=2a=8.
故|AF2|=2a-|AF1|=8-3=5.
(2)设|F1B|=k,则k>0且|AF1|=3k,|AB|=4k.由椭圆定义可得
|AF2|=2a-3k,|BF2|=2a-k.
在△ABF2中,由余弦定理可得
|AB|2=|AF2|2+|BF2|2-2|AF2|·|BF2·cos∠AF2B,
即(4k)2=(2a-3k)2+(2a-k)2-(2a-3k)· (2a-k),
化简可得(a+k)(a-3k)=0,而a+k>0,故a=3k,
于是有|AF2|=3k=|AF1|,|BF2|=5k.
因此|BF2|2=|AF2|2+|AB|2,可得F1A⊥F2A.
故△AF1F2为等腰直角三角形,
从而c=a,所以椭圆E的离心率e==.












