2014年高考数学真题Word版(文科+江西卷)
一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数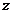 满足
满足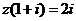 (
(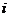 为虚数单位),则
为虚数单位),则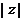 =( )
=( )
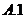
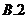
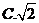
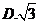
2.设全集为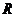 ,集合
,集合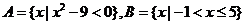 ,则
,则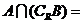 ( )
( )
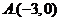
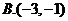
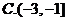
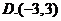
3.掷两颗均匀的骰子,则点数之和为5的概率等于( )
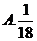
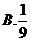
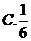
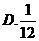
4. 已知函数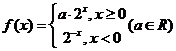 ,若
,若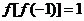 ,则
,则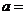 ( )
( )
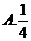
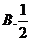
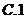
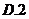
5.在在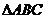 中,内角A,B,C所对应的边分别为
中,内角A,B,C所对应的边分别为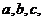 ,若
,若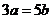 ,则
,则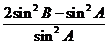 的值为( )
的值为( )
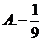
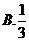
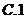
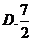
6.下列叙述中正确的是( )
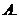 若
若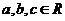 ,则
,则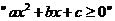 的充分条件是
的充分条件是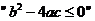
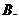 若
若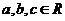 ,则
,则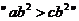 的充要条件是
的充要条件是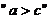
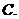 命题“对任意
命题“对任意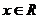 ,有
,有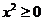 ”的否定是“存在
”的否定是“存在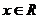 ,有
,有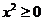 ”
”
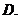
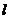 是一条直线,
是一条直线,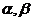 是两个不同的平面,若
是两个不同的平面,若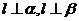 ,则
,则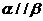
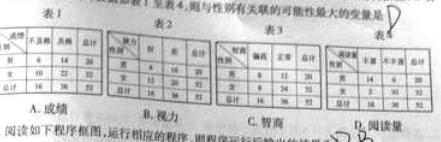
7.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,泽宇性别有关联的可能性最大的变量是( )
 9.
9.
A.成绩 B.视力 C.智商 D.阅读量
8.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )

A.7 B.9 C.10 D.11
9.过双曲线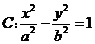 的右定点作
的右定点作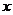 轴的垂线与
轴的垂线与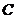 的一条渐近线相交于
的一条渐近线相交于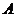 .若以
.若以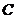 的右焦点为圆心、半径为4的圆经过
的右焦点为圆心、半径为4的圆经过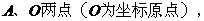 ,则双曲线
,则双曲线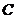 的方程为( )
的方程为( )
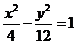 B.
B.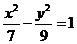 C.
C.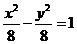 D.
D.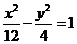
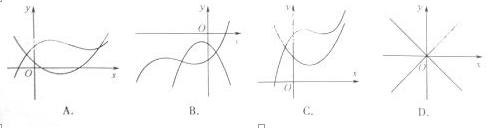
10.在同意直角坐标系中,函数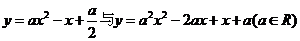 的图像不可能的是( )
的图像不可能的是( )
填空题:本大题共5小题,每小题5分,共25分.
11.若曲线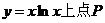 处的切线平行于直线
处的切线平行于直线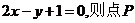 的坐标是_______.
的坐标是_______.
12.已知单位向量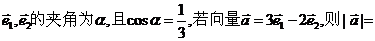 _______.
_______.
13.在等差数列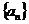 中,
中,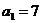 ,公差为
,公差为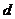 ,前
,前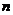 项和为
项和为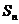 ,当且仅当
,当且仅当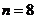 时
时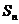 取最大值,
取最大值,
则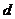 的取值范围_________.
的取值范围_________.
14.设椭圆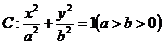 的左右焦点为
的左右焦点为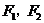 ,作
,作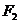 作
作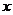 轴的垂线与
轴的垂线与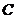 交于
交于
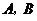 两点,
两点,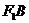 与
与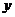 轴交于点
轴交于点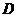 ,若
,若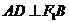 ,则椭圆
,则椭圆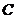 的离心率等于________.
的离心率等于________.
15.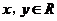 ,若
,若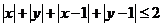 ,则
,则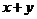 的取值范围为__________.
的取值范围为__________.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16. (本小题满分12分)
已知函数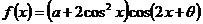 为奇函数,且
为奇函数,且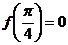 ,其中
,其中
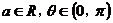 .
.
求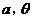 的值;
的值;
若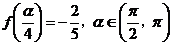 ,求
,求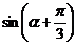 的值.
的值.
17.(本小题满分12分)
已知数列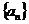 的前
的前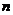 项和
项和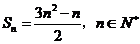 .
.
求数列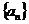 的通项公式;
的通项公式;
证明:对任意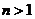 ,都有
,都有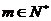 ,使得
,使得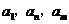 成等比数列.
成等比数列.
18.(本小题满分12分)
已知函数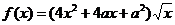 ,其中
,其中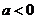 .
.
(1)当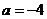 时,求
时,求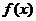 的单调递增区间;
的单调递增区间;
(2)若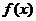 在区间
在区间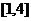 上的最小值为8,求
上的最小值为8,求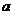 的值.
的值.
19.(本小题满分12分)
如图,三棱柱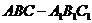 中,
中,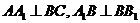 .
.
(1)求证: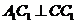 ;
;
(2)若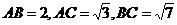 ,问
,问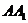 为何值时,三棱柱
为何值时,三棱柱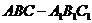 体积最
体积最
大,并求此最大值。
20.(本小题满分13分)
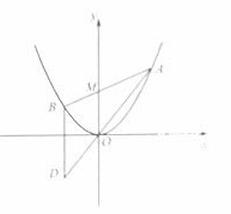
如图,已知抛物线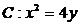 ,过点
,过点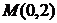 任作一直线与
任作一直线与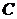 相交于
相交于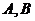 两点,过点
两点,过点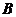 作
作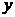 轴的平行线与直线
轴的平行线与直线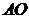 相交于点
相交于点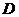 (
(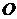 为坐标原点).
为坐标原点).
证明:动点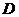 在定直线上;
在定直线上;
作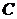 的任意一条切线
的任意一条切线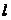 (不含
(不含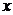 轴)与直线
轴)与直线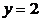 相交于点
相交于点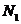 ,与(1)中的定直线相交于点
,与(1)中的定直线相交于点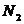 ,证明:
,证明: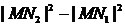 为定值,并求此定值.
为定值,并求此定值.
21.(本小题满分14分)
将连续正整数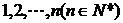 从小到大排列构成一个数
从小到大排列构成一个数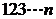 ,
,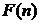 为这个数的位数(如
为这个数的位数(如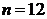 时,此数为
时,此数为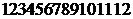 ,共有15个数字,
,共有15个数字,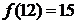 ),现从这个数中随机取一个数字,
),现从这个数中随机取一个数字,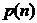 为恰好取到0的概率.
为恰好取到0的概率.
求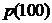 ;
;
当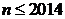 时,求
时,求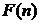 的表达式;
的表达式;
(3)令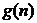 为这个数字0的个数,
为这个数字0的个数,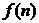 为这个数中数字9的个数,
为这个数中数字9的个数,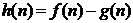 ,
,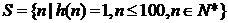 ,求当
,求当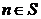 时
时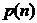 的最大值.
的最大值.












