五、（本大题2个小题，每小题10分，共20分）

22. 解:⑴ 填表:初中平均数85(分)，众数85(分)；高中部中位数80(分).

………………3分

⑵ 初中部成绩好些.因为两个队的平均数都相同，初中部的中位数高，所以在平均数相同的情况下中位数高的初中部成绩好些.

………………7分（判断正确给2分，分析合理给2分）

（3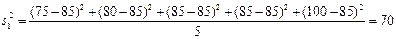）∵, …8分

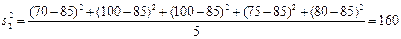.…9分

∴S12 ＜S22，因此，初中代表队选手成绩较为稳定。…………10分

23. 解：⑴总费用y1(元)和y2(元)与参演男生人数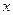之间的函数关系式分别是：

y1=0.7［120x+100(2x－100)］+2200=224x－4800 ………………2分

y2=0.8［100(3x－100)］=240x－8000 ………………4分

⑵当y1＞y2时，即224x－4800＞240x－8000，解得：x＜200 …………5分

当y1 = y2时，即224x－4800=240x－8000，解得：x=200 …………6分

当y1＜y2时，即224x－4800＜240x－8000，解得：x＞200 …………7分

即当参演男生少于200人时，购买B公司的服装比较合算；当参演男生等于200人时，购买两家公司的服装总费用相同，可任一家公司购买；当参演男生多于200人时，购买A公司的服装比较合算。 ………………10分

六、（本大题2个小题，第24题10分，第25题12分，共22分）

24. ⑴证明：∵△BCO中，BO=CO

∴∠B=BCO ………1分

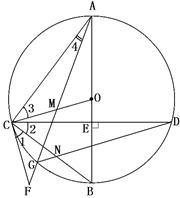
在Rt△BCE中，∠2+∠B=900

又∵∠1=∠2

∴∠1+∠BCO=900即∠FCO=900 ………2分

∴CF是⊙O的切线； ………3分

⑵证明：∵AB是⊙O直径

∴∠ACB=∠FCO=900

∴∠ACB－∠BCO=∠FCO－∠BCO

即∠3=∠1

∴∠3=∠2 …………………4分

∵∠4=∠D …………………5分

∴△ACM∽△DCN …………………6分

⑶∵⊙O的半径为4，即AO=CO=BO=4，

在Rt△COE中，COS∠BOC=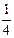

∴OE=CO·COS∠BOC=4×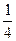=1

由此可得：BE=3，AE=5

由勾股定理可得：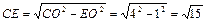

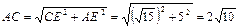
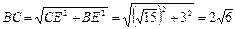…………8分

∵AB是⊙O直径，AB⊥CD

∴由垂径定理得：CD=2CE=2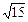

∵△ACM∽△DCN

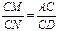∴ ……………………9分

∵点M是CO的中点，CM=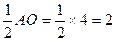

∴

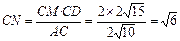
∴BN=BC－CN=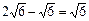 ……………………10分

25. 解：⑴∵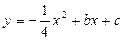经过点A(2，0)和B(0，)

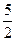∴由此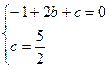得： 解得：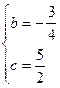

∴抛物线的解析式是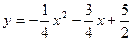 …………………2分

∵直线y=kx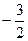经过点A(2，0)

∴2k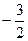=0 解得：k=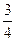

∴直线的解析式是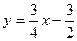 …………………3分

⑵设P的坐标是(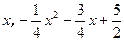)，则M的坐标是(x，)

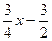∴PM=(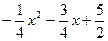)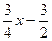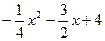－()= ……4分

解方程组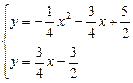 解得：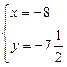

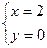
∵点D在第三象限，则点D的坐标是（－8，）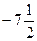

由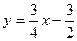得点C的坐标是(0，)

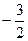∴CE=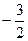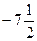－()=6 …………………5分

由于PM∥y轴，要使四边形PMEC是平行四边形，必有PM=CE，

即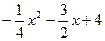=6

解这个方程得：x1=－2，x2=－4 符合－8＜x＜2 ………6分

当x1=－2时，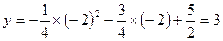

当x1=－4时，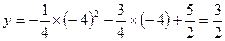

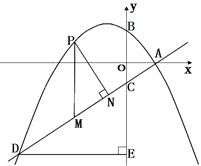
因此，直线AD上方的抛物线上存在这样的点P，使四边形PMEC是平行四边形，点P的坐标是(－2，3)和(－4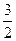，) …………………8分

⑶在Rt△CDE中，DE=8，CE=6

由勾股定理得：DC=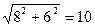

∴△CDE的周长是24 …………………9分

∵PM∥y轴，容易证明△PMN∽△CDE

∴， 即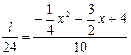…………10分

化简整理得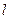：与x的函数关系式是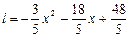： …………11分

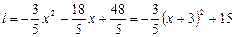
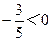∵，∴有最大值

当x=－3时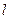，的最大值是15 …………………12分

点击此处下载文档(rar格式，239.24KB)