一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)(2013•内江)下列四个实数中,绝对值最小的数是( )
A. ﹣5 B.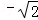 C. 1 D. 4
C. 1 D. 4
考点: 实数大小比较.
分析: 计算出各选项的绝对值,然后再比较大小即可.
解答: 解:|﹣5|=5;|﹣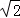 |=
|=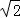 ,|1|=1,|4|=4,
,|1|=1,|4|=4,
绝对值最小的是1.
故选C.
点评: 本题考查了实数的大小比较,属于基础题,注意先运算出各项的绝对值.
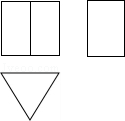
2.(3分)(2013•内江)一个几何体的三视图如图所示,那么这个几何体是( )
A.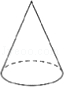 B.
B. C.
C. D.
D.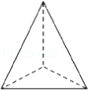
考点: 由三视图判断几何体.
分析: 由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状,即可得出答案.
解答: 解:由主视图和左视图可得此几何体为柱体,根据俯视图为三角形可得此几何体为三棱柱;
故选C.
点评: 本题考查了由三视图判断几何体,考查学生的空间想象能力,是一道基础题,难度不大.
3.(3分)(2013•内江)某公司开发一个新的项目,总投入约11500000000元,11500000000元用科学记数法表示为( )
A. 1.15×1010 B. 0.115×1011 C. 1.15×1011 D. 1.15×109
考点: 科学记数法—表示较大的数.
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解答: 解:将11500000000用科学记数法表示为:1.15×1010.
故选A.
点评: 此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(3分)(2013•内江)把不等式组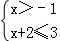 的解集表示在数轴上,下列选项正确的是( )
的解集表示在数轴上,下列选项正确的是( )
A. B.
B. C.
C. D.
D.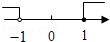
考点: 在数轴上表示不等式的解集.
分析: 求得不等式组的解集为﹣1<x≤1,所以B是正确的.
解答: 解:由第一个不等式得:x>﹣1;
由x+2≤3得:x≤1.
∴不等式组的解集为﹣1<x≤1.
故选B.
点评: 不等式组解集在数轴上的表示方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
5.(3分)(2013•内江)今年我市有近4万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A. 这1000名考生是总体的一个样本 B. 近4万名考生是总体
C. 每位考生的数学成绩是个体 D. 1000名学生是样本容量
考点: 总体、个体、样本、样本容量.
分析: 根据总体、个体、样本、样本容量的定义对各选项判断即可.
解答: 解:A、1000名考生的数学成绩是样本,故本选项错误;
B、4万名考生的数学成绩是总体,故本选项错误;
C、每位考生的数学成绩是个体,故本选项正确;
D、1000是样本容量,故本选项错误;
故选C.
点评: 本题考查了总体、个体、样本和样本容量的知识,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
6.(3分)(2013•内江)把一块直尺与一块三角板如图放置,若∠1=40°,则∠2的度数为( )
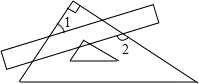
A. 125° B. 120° C. 140° D. 130°
考点: 平行线的性质;直角三角形的性质.
分析: 根据矩形性质得出EF∥GH,推出∠FCD=∠2,代入∠FCD=∠1+∠A求出即可.
解答: 解: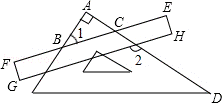
∵EF∥GH,
∴∠FCD=∠2,
∵∠FCD=∠1+∠A,∠1=40°,∠A=90°,
∴∠2=∠FCD=130°,
故选D.
点评: 本题考查了平行线性质,矩形性质,三角形外角性质的应用,关键是求出∠2=∠FCD和得出∠FCD=∠1+∠A.
7.(3分)(2013•内江)成渝路内江至成都段全长170千米,一辆小汽车和一辆客车同时从内江、成都两地相向开出,经过1小时10分钟相遇,小汽车比客车多行驶20千米.设小汽车和客车的平均速度为x千米/小时和y千米/小时,则下列方程组正确的是( )
A.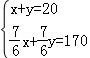 B.
B.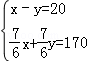
C.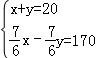 D.
D.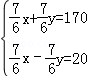
考点: 由实际问题抽象出二元一次方程组.
分析: 根据等量关系:相遇时两车走的路程之和为170千米,小汽车比客车多行驶20千米,可得出方程组.
解答: 解:设小汽车和客车的平均速度为x千米/小时和y千米/小时
由题意得,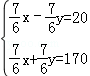 .
.
故选D.
点评: 本题考查了由实际问题抽象二元一次方程组的知识,解答本题的关键是仔细审题得到等量关系,根据等量关系建立方程.
8.(3分)(2013•内江)如图,在▱ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
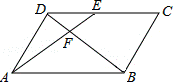
A. 2:5 B. 2:3 C. 3:5 D. 3:2
考点: 相似三角形的判定与性质;平行四边形的性质.
分析: 先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出 DE:EC的值,由AB=CD即可得出结论.
解答: 解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴DE:AB=2:5,
∵AB=CD,
∴DE:EC=2:3.
故选B.
点评: 本题考查的是相似三角形的判定与性质及平行四边形的性质,熟知相似三角形边长的比等于相似比,面积的比等于相似比的平方是解答此题的关键.
9.(3分)(2013•内江)若抛物线y=x2﹣2x+c与y轴的交点为(0,﹣3),则下列说法不正确的是( )
A. 抛物线开口向上 B. 抛物线的对称轴是x=1
C. 当x=1时,y的最大值为﹣4 D. 抛物线与x轴的交点为(﹣1,0),(3,0)
考点: 二次函数的性质.
分析: A根据二次函数二次项的系数的正负确定抛物线的开口方向.
B利用x=﹣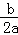 可以求出抛物线的对称轴.
可以求出抛物线的对称轴.
C利用顶点坐标和抛物线的开口方向确定抛物线的最大值或最小值.
D当y=0时求出抛物线与x轴的交点坐标.
解答: 解:∵抛物线过点(0,﹣3),
∴抛物线的解析式为:y=x2﹣2x﹣3.
A、抛物线的二次项系数为1>0,抛物线的开口向上,正确.
B、根据抛物线的对称轴x=﹣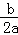 =﹣
=﹣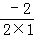 =1,正确.
=1,正确.
C、由A知抛物线的开口向上,二次函数有最小值,当x=1时,y的最小值为﹣4,而不是最大值.故本选项错误.
D、当y=0时,有x2﹣2x﹣3=0,解得:x1=﹣1,x2=3,抛物线与x轴的交点坐标为(﹣1,0),(3,0).正确.
故选C.
点评: 本题考查的是二次函数的性质,根据a的正负确定抛物线的开口方向,利用顶点坐标公式求出抛物线的对称轴和顶点坐标,确定抛物线的最大值或最小值,当y=0时求出抛物线与x轴的交点坐标.
10.(3分)(2013•内江)同时抛掷A、B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x、y,并以此确定点P(x,y),那么点P落在抛物线y=﹣x2+3x上的概率为( )
A.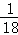 B.
B.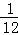 C. D.
C. D.
考点: 列表法与树状图法;二次函数图象上点的坐标特征.
专题: 阅读型.
分析: 画出树状图,再求出在抛物线上的点的坐标的个数,然后根据概率公式列式计算即可得解.
解答: 解:根据题意,画出树状图如下:
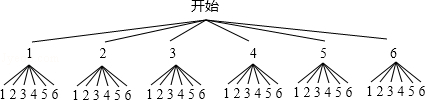
一共有36种情况,
当x=1时,y=﹣x2+3x=﹣12+3×1=2,
当x=2时,y=﹣x2+3x=﹣22+3×2=2,
当x=3时,y=﹣x2+3x=﹣32+3×3=0,
当x=4时,y=﹣x2+3x=﹣42+3×4=﹣4,
当x=5时,y=﹣x2+3x=﹣52+3×5=﹣10,
当x=6时,y=﹣x2+3x=﹣62+3×6=﹣18,
所以,点在抛物线上的情况有2种,
P(点在抛物线上)=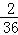 =
=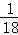 .
.
故选A.
点评: 本题考查了列表法与树状图法,二次函数图象上点的坐标特征,用到的知识点为:概率=所求情况数与总情况数之比.
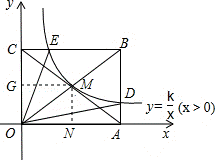
11.(3分)(2013•内江)如图,反比例函数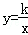 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
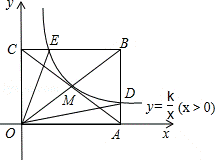
A. 1 B. 2 C. 3 D. 4
考点: 反比例函数系数k的几何意义.
专题: 数形结合.
分析: 本题可从反比例函数图象上的点E、M、D入手,分别找出△OCE、△OAD、矩形OABC的面积与|k|的关系,列出等式求出k值.
解答: 解:由题意得:E、M、D位于反比例函数图象上,则S△OCE=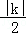 ,S△OAD=
,S△OAD=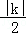 ,
,
过点M作MG⊥y轴于点G,作MN⊥x轴于点N,则S□ONMG=|k|,
又∵M为矩形ABCO对角线的交点,
∴S矩形ABCO=4S□ONMG=4|k|,
由于函数图象在第一象限,k>0,则++9=4k,
解得:k=3.
故选C.
点评: 本题考查反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,本知识点是中考的重要考点,同学们应高度关注.
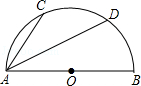
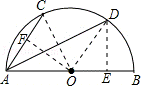
12.(3分)(2013•内江)如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.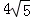 cm B.
cm B.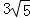 cm C.
cm C.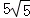 cm D. 4cm
cm D. 4cm
考点: 圆心角、弧、弦的关系;全等三角形的判定与性质;勾股定理.
分析: 连接OD,OC,作DE⊥AB于E,OF⊥AC于F,运用圆周角定理,可证得∠DOB=∠OAC,即证△AOF≌△OED,所以OE=AF=3cm,根据勾股定理,得DE=4cm,在直角三角形ADE中,根据勾股定理,可求AD的长.
解答: 解:连接OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴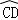 =
=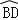 ,
,
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△OED,
∴OE=AF=AC=3cm,
在Rt△DOE中,DE=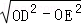 =4cm,
=4cm,
在Rt△ADE中,AD=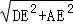 =4
=4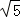 cm.
cm.
故选A.
点评: 本题考查了翻折变换及圆的有关计算,涉及圆的题目作弦的弦心距是常见的辅助线之一,注意熟练运用垂径定理、圆周角定理和勾股定理.












