一、选择题:本大题共10小题,每小题3分,共30分.每小题给出的四个选项中,只有一项是符合题目要求的,请将符合题意的选项字母填入题后的括号内
1.(3分)(2013•白银)3的相反数是( )
A. 3 B. ﹣3 C. D. ﹣
考点: 相反数.
分析: 根据相反数的意义,3的相反数即是在3的前面加负号.
解答: 解:根据相反数的概念及意义可知:3的相反数是﹣3.
故选B.
点评: 本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.
2.(3分)(2013•白银)下列运算中,结果正确的是( )
A. 4a﹣a=3a B. a10÷a2=a5 C. a2+a3=a5 D. a3•a4=a12
考点: 同底数幂的除法;合并同类项;幂的乘方与积的乘方.
专题: 计算题.
分析: 根据合并同类项、同底数幂的除法法则:底数不变,指数相减,同底数幂的乘法法则:底数不变,指数相加,可判断各选项.
解答: 解:A、4a﹣a=3a,故本选项正确;
B、a10÷a2=a10﹣2=a8≠a5,故本选项错误;
C、a2+a3≠a5,故本选项错误;
D、根据a3•a4=a7,故a3•a4=a12本选项错误;
故选A.
点评: 此题考查了同类项的合并,同底数幂的乘除法则,属于基础题,解答本题的关键是掌握每部分的运算法则,难度一般.
3.(3分)(2013•白银)下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
考点: 中心对称图形.
分析: 根据中心对称图形的定义旋转180°后能够与原图形完全重合即是中心对称图形,即可判断出.
解答: 解:∵A.此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,故此选项错误;
B:∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,故此选项错误;
C.此图形旋转180°后能与原图形重合,此图形是中心对称图形,故此选项正确;
D:∵此图形旋转180°后不能与原图形重合,∴此图形不是中心对称图形,故此选项错误.
故选C.
点评: 此题主要考查了中心对称图形的定义,根据定义得出图形形状是解决问题的关键.
4.(3分)(2013•白银)如图是由两个小正方体和一个圆锥体组成的立体图形,其主视图是( )
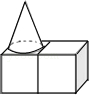
A.  B.
B.  C.
C.  D.
D. 
考点: 简单组合体的三视图.
分析: 主视图是从正面看,注意所有的看到的棱都应表现在主视图中.
解答: 解:从正面看,圆锥看见的是:三角形,两个正方体看见的是两个正方形.
故答案为B.
点评: 此题主要考查了三视图的知识,关键是掌握三视图的几种看法.
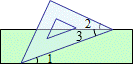
5.(3分)(2013•白银)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
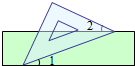
A. 15° B. 20° C. 25° D. 30°
考点: 平行线的性质.
分析: 根据两直线平行,内错角相等求出∠3,再求解即可.
解答: 解:∵直尺的两边平行,∠1=20°,
∴∠3=∠1=20°,
∴∠2=45°﹣20°=25°.
故选C.
点评: 本题考查了两直线平行,内错角相等的性质,是基础题,熟记性质是解题的关键.
6.(3分)(2013•白银)一元二次方程x2+x﹣2=0根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 无实数根 D. 无法确定
考点: 根的判别式.
分析: 判断上述方程的根的情况,只要看根的判别式△=b2﹣4ac的值的符号就可以了.
解答: 解:∵a=1,b=1,c=﹣2,
∴△=b2﹣4ac=1+8=9>0
∴方程有两个不相等的实数根.
故选A
点评: 本题考查了一元二次方程根的判别式的应用.
总结:一元二次方程根的情况与判别式△的关系:
(1)△>0⇔方程有两个不相等的实数根;
(2)△=0⇔方程有两个相等的实数根;
(3)△<0⇔方程没有实数根.
7.(3分)(2013•白银)分式方程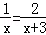 的解是( )
的解是( )
A. x=﹣2 B. x=1 C. x=2 D. x=3
考点: 解分式方程.
分析: 公分母为x(x+3),去括号,转化为整式方程求解,结果要检验.
解答: 解:去分母,得x+3=2x,
解得x=3,
当x=3时,x(x+3)≠0,
所以,原方程的解为x=3,
故选D.
点评: 本题考查了解分式方程.(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,(2)解分式方程一定注意要验根.
8.(3分)(2013•白银)某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )
A. 48(1﹣x)2=36 B. 48(1+x)2=36 C. 36(1﹣x)2=48 D. 36(1+x)2=48
考点: 由实际问题抽象出一元二次方程.
专题: 增长率问题.
分析: 三月份的营业额=一月份的营业额×(1+增长率)2,把相关数值代入即可.
解答: 解:二月份的营业额为36(1+x),
三月份的营业额为36(1+x)×(1+x)=36(1+x)2,
即所列的方程为36(1+x)2=48,
故选D.
点评: 考查列一元二次方程;得到三月份的营业额的关系是解决本题的关键.
9.(3分)(2013•白银)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
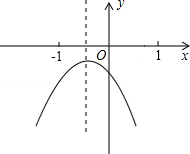
A. 1个 B. 2个 C. 3个 D. 4个
考点: 二次函数图象与系数的关系.
分析: 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,利用图象将x=1,﹣1,2代入函数解析式判断y的值,进而对所得结论进行判断.
解答: 解:①∵由函数图象开口向下可知,a<0,由函数的对称轴x=﹣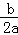 <0,故b>0,所以2a﹣b<0,①正确;
<0,故b>0,所以2a﹣b<0,①正确;
②∵a<0,对称轴在y轴左侧,a,b同号,图象与y轴交于负半轴,则c<0,故abc<0;②正确;
③当x=1时,y=a+b+c<0,③正确;
④当x=﹣1时,y=a﹣b+c<0,④错误;
⑤当x=2时,y=4a+2b+c<0,⑤错误;
故错误的有2个.
故选:B.
点评: 此题主要考查了图象与二次函数系数之间的关系,将x=1,﹣1,2代入函数解析式判断y的值是解题关键.
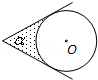
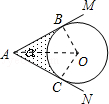
10.(3分)(2013•白银)如图,⊙O的圆心在定角∠α(0°<α<180°)的角平分线上运动,且⊙O与∠α的两边相切,图中阴影部分的面积S关于⊙O的半径r(r>0)变化的函数图象大致是( )
A. 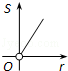 B.
B. 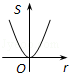 C.
C. 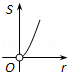 D.
D. 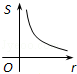
考点: 动点问题的函数图象;多边形内角与外角;切线的性质;切线长定理;扇形面积的计算;锐角三角函数的定义.
专题: 计算题.
分析: 连接OB、OC、OA,求出∠BOC的度数,求出AB、AC的长,求出四边形OBAC和扇形OBC的面积,即可求出答案.
解答: 解:连接OB、OC、OA,
∵圆O切AM于B,切AN于C,
∴∠OBA=∠OCA=90°,OB=OC=r,AB=AC
∴∠BOC=360°﹣90°﹣90°﹣α=(180﹣α)°,
∵AO平分∠MAN,
∴∠BAO=∠CAO=α,
AB=AC=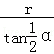 ,
,
∴阴影部分的面积是:S四边形BACO﹣S扇形OBC=2××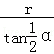 ×r﹣
×r﹣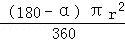 =(
=(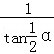 ﹣
﹣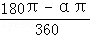 )r2,
)r2,
∵r>0,
∴S与r之间是二次函数关系.
故选C.
点评: 本题主要考查对切线的性质,切线长定理,三角形和扇形的面积,锐角三角函数的定义,四边形的内角和定理等知识点的理解和掌握,能综合运用性质进行计算是解此题的关键.












