一.选择题(本大题共有8小题,每小题2分,共16分,在每小题所给的四个选项中,只有一项是正确的)
1.(2分)(2013•常州)在下列实数中,无理数是( )
A. 2 B. 3.14 C.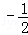 D.
D.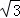
考点: 无理数.
分析: 根据无理数,有理数的定义对各选项分析判断后利用排除法求解.
解答: 解:A、2是有理数,故本选项错误;
B、3.14是有理数,故本选项错误;
C、﹣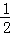 是有理数,故本选项错误;
是有理数,故本选项错误;
D、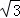 是无理数,故本选项正确.
是无理数,故本选项正确.
故选D.
点评: 主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.
2.(2分)(2013•常州)如图所示圆柱的左视图是( )

A. B.
B.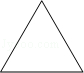 C.
C. D.
D.
考点: 简单几何体的三视图 8684
分析: 找到从左面看所得到的图形即可.
解答: 解:此圆柱的左视图是一个矩形,故选C.
点评: 本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
3.(2分)(2013•常州)下列函数中,图象经过点(1,﹣1)的反比例函数关系式是( )
A.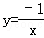 B.
B.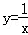 C.
C.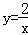 D.
D.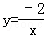
考点: 反比例函数图象上点的坐标特征
分析: 设将点(1,﹣1)代入所设的反比例函数关系式y=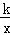 (k≠0)即可求得k的值.
(k≠0)即可求得k的值.
解答: 解:设经过点(1,﹣1)的反比例函数关系式是y=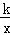 (k≠0),则﹣1=
(k≠0),则﹣1=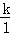 ,
,
解得,k=﹣1,
所以,所求的函数关系式是y=﹣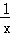 或
或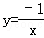 .
.
故选A.
点评: 本题主要考查反比例函数图象上点的坐标特征.所有反比例函数图象上点的坐标都满足该函数解析式.
4.(2分)(2013•常州)下列计算中,正确的是( )
A. (a3b)2=a6b2 B. a•a4=a4 C. a6÷a2=a3 D. 3a+2b=5ab
考点: 同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.
分析: 根据积的乘方,等于把每一个因式分别乘方,再把所得的幂相乘;同底数幂相乘,底数不变指数相加;同底数幂相除,底数不变指数相减对各选项分析判断后利用排除法求解.
解答: 解:A、(a3b)2=a6b2,故本选项正确;
B、a•a4=a5,故本选项错误;
C、a6÷a2=a6﹣2=a4,故本选项错误;
D、3a与2b不是同类项,不能合并,故本选项错误.
故选A.
点评: 本题考查了同底数幂的除法,同底数幂的乘法,积的乘方的性质,理清指数的变化是解题的关键.
5.(2分)(2013•常州)已知:甲乙两组数据的平均数都是5,甲组数据的方差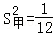 ,乙组数据的方差
,乙组数据的方差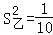 ,下列结论中正确的是( )
,下列结论中正确的是( )
A. 甲组数据比乙组数据的波动大
B. 乙组数据的比甲组数据的波动大
C. 甲组数据与乙组数据的波动一样大
D. 甲组数据与乙组数据的波动不能比较
考点: 方差.
分析: 方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,结合选项进行判断即可.
解答: 解:由题意得,方差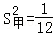 <
<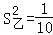 ,
,
A、甲组数据没有乙组数据的波动大,故本选项错误;
B、乙组数据的比甲组数据的波动大,说法正确,故本选项正确;
C、甲组数据没有乙组数据的波动大,故本选项错误;
D、甲组数据没有乙组数据的波动大,故本选项错误;
故选B.
点评: 本题考查了方差的意义,解答本题的关键是理解方差的意义,方差表示的是数据波动性的大小,方差越大,波动性越大.
6.(2分)(2013•常州)已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )
A. 相离 B. 相切 C. 相交 D. 无法判断
考点: 直线与圆的位置关系.
分析: 根据圆O的半径和圆心O到直线l的距离的大小,相交:d<r;相切:d=r;相离:d>r;即可选出答案.
解答: 解:∵⊙O的半径为6,圆心O到直线l的距离为5,
∵6>5,即:d<r,
∴直线L与⊙O的位置关系是相交.
故选;C.
点评: 本题主要考查对直线与圆的位置关系的性质的理解和掌握,能熟练地运用性质进行判断是解此题的关键.
7.(2分)(2013•常州)二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;
(2)当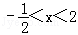 时,y<0;
时,y<0;
(3)二次函数y=ax2+bx+c的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是( )
A. 3 B. 2 C. 1 D. 0
考点: 二次函数的最值;抛物线与x轴的交点.
分析: 根据表格数据求出二次函数的对称轴为直线x=1,然后根据二次函数的性质对各小题分析判断即可得解.
解答: 解;由表格数据可知,二次函数的对称轴为直线x=1,
所以,当x=1时,二次函数y=ax2+bx+c有最小值,最小值为﹣4;故(1)小题错误;
根据表格数据,当﹣1<x<3时,y<0,
所以,﹣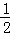 <x<2时,y<0正确,故(2)小题正确;
<x<2时,y<0正确,故(2)小题正确;
二次函数y=ax2+bx+c的图象与x轴有两个交点,分别为(﹣1,0)(3,0),它们分别在y轴两侧,故(3)小题正确;
综上所述,结论正确的是(2)(3)共2个.
故选B.
点评: 本题考查了二次函数的最值,抛物线与x轴的交点,仔细分析表格数据,熟练掌握二次函数的性质是解题的关键.
8.(2分)(2013•常州)有3张边长为a的正方形纸片,4张边长分别为a、b(b>a)的矩形纸片,5张边长为b的正方形纸片,从其中取出若干张纸片,每种纸片至少取一张,把取出的这些纸片拼成一个正方形(按原纸张进行无空隙、无重叠拼接),则拼成的正方形的边长最长可以为( )
A. a+b B. 2a+b C. 3a+b D. a+2b
考点: 完全平方公式的几何背景.
分析: 根据3张边长为a的正方形纸片的面积是3a2,4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,5张边长为b的正方形纸片的面积是5b2,得出a2+4ab+4b2=(a+2b)2,再根据正方形的面积公式即可得出答案.
解答: 解;3张边长为a的正方形纸片的面积是3a2,
4张边长分别为a、b(b>a)的矩形纸片的面积是4ab,
5张边长为b的正方形纸片的面积是5b2,
∵a2+4ab+4b2=(a+2b)2,
∴拼成的正方形的边长最长可以为(a+2b),
故选D.
点评: 此题考查了完全平方公式的几何背景,关键是根据题意得出a2+4ab+4b2=(a+2b)2,用到的知识点是完全平方公式.
二.填空题(本大题共有9小题,第9小题4分,其余8小题每小题4分,共20分,)
9.(4分)(2013•常州)计算﹣(﹣3)= 3 ,|﹣3|= 3 ,(﹣3)﹣1= ﹣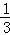 ,(﹣3)2= 9 .
,(﹣3)2= 9 .
考点: 有理数的乘方;相反数;绝对值;有理数的减法.
分析: 根据相反数的定义,绝对值的性质,负整数指数幂,有理数的乘方的意义分别进行计算即可得解.
解答: 解:﹣(﹣3)=3,
|﹣3|=3,
(﹣3)﹣1=﹣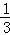 ,
,
(﹣3)2=9.
故答案为:3;3;﹣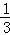 ;9.
;9.
点评: 本题考查了相反数的定义,绝对值的性质,负整数指数幂,以及有理数的乘方的意义,是基础题.
10.(2分)(2013•常州)已知点P(3,2),则点P关于y轴的对称点P1的坐标是 (﹣3,2) ,点P关于原点O的对称点P2的坐标是 (﹣3,﹣2) .
考点: 关于原点对称的点的坐标;关于x轴、y轴对称的点的坐标.
分析: 根据关于y轴对称的点的横坐标互为相反数,纵坐标相同;
关于原点对称的点的横坐标与纵坐标都互为相反数解答.
解答: 解:点P(3,2)关于y轴的对称点P1的坐标是(﹣3,2),
点P关于原点O的对称点P2的坐标是(﹣3,﹣2).
故答案为:(﹣3,2);(﹣3,﹣2).
点评: 本题考查了关于原点对称点点的坐标,关于y轴对称的点的坐标,熟记对称点的坐标特征是解题的关键.
11.(2分)(2013•常州)已知一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,﹣2)和点B(1,0),则k= 2 ,b= ﹣2 .
考点: 待定系数法求一次函数解析式.
分析: 把点A、B的坐标代入函数解析式,利用待定系数法求一次函数解析式解答即可.
解答: 解:∵一次函数y=kx+b(k、b为常数且k≠0)的图象经过点A(0,﹣2)和点B(1,0),
∴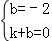 ,
,
解得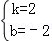 .
.
故答案为:2,﹣2.
点评: 本题主要考查了待定系数法求一次函数解析式,待定系数法是求函数解析式常用的方法之一,要熟练掌握并灵活运用.
12.(2分)(2013•常州)已知扇形的半径为6cm,圆心角为150°,则此扇形的弧长是 5π cm,扇形的面积是 15π cm2(结果保留π).
考点: 扇形面积的计算;弧长的计算.
分析: 根据扇形的弧长公式l=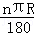 和扇形的面积=
和扇形的面积=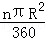 ,分别进行计算即可.
,分别进行计算即可.
解答: 解:∵扇形的半径为6cm,圆心角为150°,
∴此扇形的弧长是:l=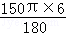 =5π(cm),
=5π(cm),
根据扇形的面积公式,得
S扇=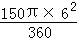 =15π(cm2).
=15π(cm2).
故答案为:5π,15π.
点评: 此题主要考查了扇形弧长公式以及扇形面积公式的应用,熟练记忆运算公式进行计算是解题关键.
13.(2分)(2013•常州)函数y=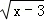 中自变量x的取值范围是 x≥3 ;若分式
中自变量x的取值范围是 x≥3 ;若分式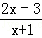 的值为0,则x=
的值为0,则x= 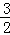 .
.
考点: 分式的值为零的条件;函数自变量的取值范围.
分析: 根据被开方数大于等于0列式计算即可得解;
根据分式的值为0,分子等于0,分母不等于0列式计算即可得解.
解答: 解:根据题意得,x﹣3≥0,
解得x≥3;
2x﹣3=0且x+1≠0,
解得x=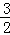 且x≠﹣1,
且x≠﹣1,
所以,x=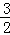 .
.
故答案为:x≥3;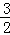 .
.
点评: 本题主要考查了分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.
14.(2分)(2013•常州)我市某一周的每一天的最高气温统计如下表:
最高气温(℃) 25 26 27 28
天数 1 1 2 3
则这组数据的中位数是 27 ,众数是 28 .
考点: 众数;中位数.
分析: 根据中位数、众数的定义,结合表格信息即可得出答案.
解答: 解:将表格数据从大到小排列为:25,26,27,27,28,28,28,
中位数为:27;
众数为:28.
故答案为:27、28.
点评: 本题考查了众数、中位数的定义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
15.(2分)(2013•常州)已知x=﹣1是关于x的方程2x2+ax﹣a2=0的一个根,则a= ﹣2或1 .
考点: 一元二次方程的解.
分析: 方程的解就是能使方程左右两边相等的未知数的值,把x=﹣1代入方程,即可得到一个关于a的方程,即可求得a的值.
解答: 解:根据题意得:2﹣a﹣a2=0
解得a=﹣2或1
点评: 本题主要考查了方程的解得定义,是需要掌握的基本内容.
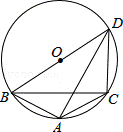
16.(2分)(2013•常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= 2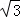 .
.
考点: 圆周角定理;含30度角的直角三角形;勾股定理;圆心角、弧、弦的关系.
分析: 根据直径所对的圆周角是直角可得∠BAD=∠BCD=90°,然后求出∠CAD=30°,利用同弧所对的圆周角相等求出∠CBD=∠CAD=30°,根据圆内接四边形对角互补求出∠BDC=60°再根据等弦所对的圆周角相等求出∠ADB=∠ADC,从而求出∠ADB=30°,解直角三角形求出BD,再根据直角三角形30°角所对的直角边等于斜边的一半解答即可.
解答: 解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=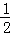 ∠BDC=
∠BDC=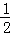 ×60°=30°,
×60°=30°,
∵AD=6,
∴在Rt△ABD中,BD=AD÷cos60°=6÷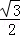 =4
=4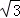 ,
,
在Rt△BCD中,DC=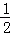 BD=
BD=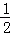 ×4
×4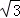 =2
=2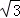 .
.
故答案为:2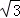 .
.
点评: 本题考查了圆周角定理,直角三角形30°角所对的直角边等于斜边的一半,以及圆的相关性质,熟记各性质是解题的关键.
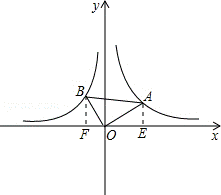
17.(2分)(2013•常州)在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数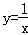 的图象上,第二象限内的点B在反比例函数
的图象上,第二象限内的点B在反比例函数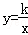 的图象上,连接OA、OB,若OA⊥OB,OB=
的图象上,连接OA、OB,若OA⊥OB,OB=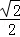 OA,则k= ﹣
OA,则k= ﹣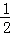 .
.
考点: 反比例函数综合题.
分析: 过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,设点A的坐标为(a,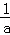 ),点B的坐标为(b,
),点B的坐标为(b,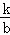 ),判断出△OBF∽△AOE,利用对应边成比例可求出k的值.
),判断出△OBF∽△AOE,利用对应边成比例可求出k的值.
解答: 解:过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
设点A的坐标为(a,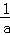 ),点B的坐标为(b,
),点B的坐标为(b,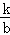 ),
),
∵∠AOE+∠BOF=90°,∠OBF+∠BOF=90°,
∴∠AOE=∠OBF,
又∵∠BFO=∠OEA=90°,
∴△OBF∽△AOE,
∴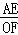 =
=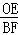 =
=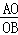 ,即
,即 =
=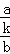 =
=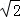 ,
,
则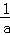 =﹣
=﹣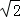 b①,a=
b①,a=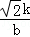 ②,
②,
①×②可得:﹣2k=1,
解得:k=﹣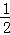 .
.
故答案为:﹣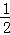 .
.
点评: 本题考查了反比例函数的综合题,涉及了相似三角形的判定与性质,反比例函数图象上点的坐标的特点,解答本题要求同学们能将点的坐标转化为线段的长度.












