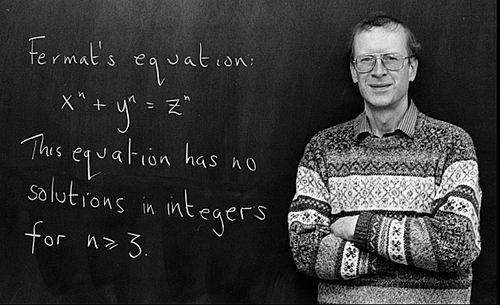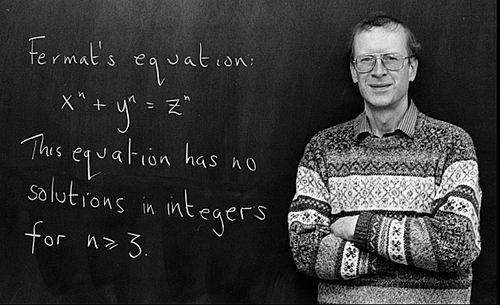I think it will always stand as one of the high achievements of number theory.
我认为这将一直是数论领域中的最高成就之一。
It was magnificent.
太了不起了
It's not every day that you hear the proof of the century.
不是每一天都能听说到世纪之证明的
Well my first reaction was: I told you so.
我第一反应就是:我告诉过你。
The Taniyama-Shimura conjecture is no longer a conjecture,
谷山-志村猜想不再是个猜想,
and as a result Fermat's last theorem has been proved.
结局就是费马的最后定理终被证明。
But is Andrew's proof the same as Fermat's?
但安德鲁的证明和费马的是一样的吗?
Fermat couldn't possibly have had this proof. It's a 20th-century proof.
费马不可能有这样的证明,因为这是个20世纪的证明。
There's no way this could have been done before the 20th-century.
而这不可能在20世纪之前就可得以做到。
I'm relieved that this result is now settled.
这个结果现终取得,我感到释然。
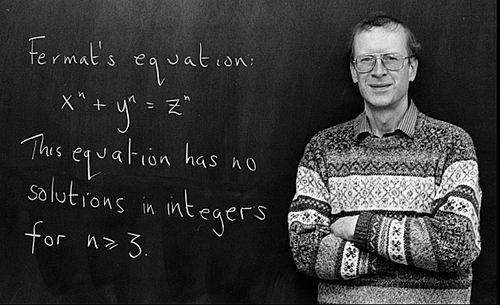
But I'm sad in some ways because Fermat's last theorem has been responsible for so much.
但在某些方面又难过,因为费马最后定理如此意义菲然。
What will we find to take its place?
我们将找到什么来取代它的位置呢?
There's no other problem that will mean the same to me.
没有其它的难题对我来说具有同等意义
I had this very rare privilege of being able to pursue in my adult life what had been my childhood dream.
我有过这难得的荣幸,能够在我的成年年岁中追寻我儿时的梦想。
I know it's a rare privilege but if one can do this it's more rewarding than anything I could imagine.
我知道那是难得的荣幸,但如果可做成,就将比我所能想象的任何事情都有价值。
One of the great things about this work is it embraces the ideas of so many mathematicians.
这项工作中了不起的一件事就是,它包涵了如此多数学家的思想。
I've made a partial list: Klein, Fricke, Hurwitz, Hecke, Dirichlet, Dedekind...
我列出个不完整的名单:克莱茵,弗里克,胡尔维茨,赫克,狄利克莱,戴德金...
The proof by Langlands and Tunnell... Deligne, Rapoport, Katz...
包括朗兰兹和图内尔,德里格内,拉波波特,凯兹的证明...
Mazur's idea of using the deformation theory of Galois representations...
包括梅休尔使用伽罗华表示之变形理论的想法...
Igusa, Eichler, Shimura, Taniyama... Frey's reduction...
依古瑟,埃其勒,志村五郎,谷山丰...弗莱的整理...
The list goes on and on... Bloch, Kato, Selmer, Frey, Fermat.
这个名单还长得很...布洛克,卡特,塞尔默,弗莱,费马。